Digital Electronics में Boolean algebra का मुख्य उद्देश्य किसी भी expression या equation को simplify/reduce करना है. इसको जॉर्ज बूले ने 1984 में introduce किया।
Boolean Algebra का उपयोग Switching Circuits, Computer और Physics आदि में किया जाता है.
Mathematical Algebra की तरह Boolean Algebra के भी नियम (law/rules) हैं. जिनकी मदद से किसी भी boolean expression को reduce या simplify कर सकते हैं. उदाहरण के लिए,
Y = A’BC+ABC+AB’C’+AB’C+ABC’ Expression को Simplify करें।
Y = BC (A’+A) +AB’ (C’+C) + ABC’ (1)
OR Law से, (A’+A) = 1 और (C’+C) = 1
Equation (1) में मान रखने पर,
Y = BC + AB’ + ABC’
ऊपर लिखी गई equation को rearrange करने पर,
Y = AB’ + BC + ABC’
Y = AB’ + B (C + AC’)
Distributive Law से,
Y = AB’+ B (C + A) (C + C’)
हम जानते हैं की, C + C’ = 1
Y = AB’ + B (C+A)
Y = AB’ + BC + AB
Y = AB’ + AB + BC
Y = A (B’+B) + BC
Y = A + BC
ऊपर लिखे गए उदाहरण से आप समझ गए होंगे की कैसे यह नियम किसी भी expression को reduce करने में मदद करते हैं.
जितना छोटा expression होगा, उतने ही कम logic gates प्रयोग होंगे और उतने ही कम components जैसे- Diode, Zener Diode, Capacitor, Resistor का उपयोग होगा।
कम components का उपयोग करने से Device का price भी कम हो जायेगा।
आइये, Boolean Algebra’s Law और Demorgan’s Theorem को समझते हैं.
Basic Laws of Boolean Algebra in Hindi
इस आर्टिकल में, बूलियन algebra से जुड़े कुछ basic laws बतायें है,
What is Complement Law in Boolean Algebra in Hindi?
यह नियम ‘0’ को ‘1’ और ‘1’ को ‘0’ में बदलता है.
A = A’
B = B’
अगर आप Complement A का complement लेते हैं, तो output A प्राप्त होगा। इसे double inversion of variable या inversion law भी कहते हैं.
(A’)’ = A
- Hexadecimal Number System in Hindi
- Octal Number System in Hindi
- Binary Number System in Hindi
- Decimal Number System in Hindi
What is Commutative Law in Boolean Algebra?
इस नियम के अनुसार, variables का order या sequence बदलने पर भी आउटपुट same ही प्राप्त होता है.
A + B = B + A (Commutative Law of Addition)
A.B = B.A (Commutative Law of Multiplication)
इन equation को Truth-table की मदद से Check करते हैं की A + B, B + A के बराबर है या नहीं।
| Input A | Input B | A+B | B + A |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
Truth-Table से यह सिद्ध होता है, की variables का order बदलने पर भी output, same ही प्राप्त होता है.
What is Associative Law of Boolean Algebra?
A + (B + C) = (A + B) + C (Associative Law of Addition)
A . (B.C) = (A.B) .C (Associative Law of Multiplication)
ऊपर लिखी गई समीकरण को truth table से check करते हैं की इनका आउटपुट बदलता है या नहीं।
| Input A | Input B | Input C | (B + C) | A + (B+C) | (A +B) | (A +B) +C |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Truth table से यह सिद्ध होता है की A + (B + C) का output और (A + B) + C का output समान है.
What is Distributive Law of Boolean Algebra?
यह नियम brackets में लिखे गए Expression को solve करता है.
A + (B.C) = (A + B).(A+C)
A. (B + C) = A.B + A.C
What is AND Law in Boolean Algebra?
यह नियम ‘AND Operation’ perform करता है.
- A . 0 = 0
- A . 1 = A
- A . A = A
- A . A’ = 0
What is OR Law in Boolean Algebra?
यह नियम ‘OR Operation’ perform करता है.
- A + 0 = A
- A + 1 = 1
- A + A = A
- A + A’ = 1
ऊपर बताये गए नियमों (law) का उपयोग करते हुए सिद्द करें, A + A . B = A’
OR Law के अनुसार, B + B’ =1
=A (B + B’) + A . B
= A . B + A . B’ + A . B
हम जानते हैं की, A + A = A
= A . B + A. B’
= A (B + B’)
= A
State and Prove DeMorgan Theorem in Boolean Algebra in Hindi?
प्रसिद्द गणितज्ञ Demorgan ने Boolean Expressions को reduce या simplify करने के लिए दो theorem प्रस्तुत की.
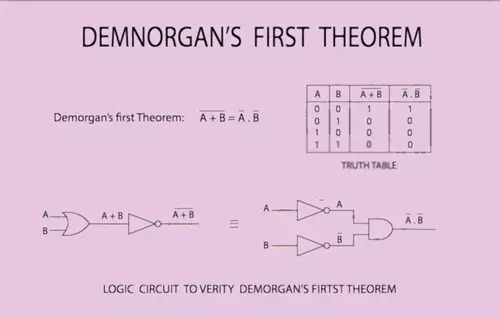
Theorem-1: Demorgan की पहली theorem के अनुसार, दो या दो से अधिक Variables के product का Complement, Complement Variables के योग के बराबर होता है.
(A.B)’ = A’ + B’
Proof: (A.B)’ = A’ + B’, Equation को Truth-Table की मदद से proof करते हैं की, (A.B)’ का आउटपुट, A’ + B’ के आउटपुट के बराबर है या नहीं।
| Input A | Input B | A.B | (A.B)’ | A’ | B’ | A’ + B’ |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
अगर, आप Red Marked दोनों Coloumns को ध्यान से देखें, तो आप पाएंगे की (A.B)’ का आउटपुट, A’ + B’ के बराबर है.
De morgan Theorem Proof:
AND Law और OR Law से हम जानते हैं की, A.A’= 0 और A + A’ = 1 होता है.
माना, P = A + B और P’ = A’.B’, तो सिद्ध करें, P + P’ = 1 और P . P’ = 0.
Case- 1: सिद्द करें, P + P’ = 1.
P’ का मान P + P’ = 1 equation में रखने पर,
P + A’ . B’ = 1
Distributive Law के अनुसार,
(P +A’) . (P + B’) = 1
P का मान ऊपर लिखी गई equation में रखने पर,
(A + B + A’).(A+B+B’)=1, From OR Law (A +A’) =1
(1 + B) . (A + 1) =1
हम जानते हैं की, (1 +B) =1 और (1 + A)=1
1.1 =1
1=1
Case-2: सिद्द करें, P.P’ =0
= (A + B) . (A’.B’)
= (A.A’.B’) + (A.A’.B’)
= 0 + 0
= 0
Theorem-2: इस theorem के अनुसार, दो या दो से अधिक variables के योग का complement, variables के complement के product के बराबर होता है.
(A + B)’ = A’ . B’
De Morgan Theorem Proof: आइये, Truth-table की मदद से check करते हैं की (A + B)’ का आउटपुट, A’ . B’ के आउटपुट के बराबर है या नहीं।
| Input A | Input B | (A + B) | (A + B)’ | A’ | B’ | (A’.B’) |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
यदि आप Truth-table में red marked column को ध्यान से देखें, आप पाते हैं की (A + B)’ का output, (A’.B’) के output के बराबर है.
De morgan Theorem Proof
Case-1: सिद्ध करें, P + P’ =1
माना, P = A.B और P’= A’ +B’ है.
Equation P + P’ = 1 में, P का मान रखने पर,
=A . B + P’
Distributive Law के अनुसार,
= (P’ + A) . (P’ + B)
P’ की value equation में रखने पर,
= (A’ + B’ + A) . (A’ + B’ +B)
= (A’+A+B’). (A’+B+B’)
हम जानते हैं की, B + B’ =1 और (A+A’) =1
= (1+B’) . (A’+1)
=1.1
=1
Case 2: सिद्द करें, P.P’=0
माना , P = A.B और P’ = A’ + B’
= A.B. (A’ + B’)
= A.B.A’ + A.B.B’
= 0 + 0
=0
मुझे उम्मीद है की इस आर्टिकल में आपको Basic Laws of Boolean Algebra in Hindi में सीखने और समझने को मिला होगा। यदि आपका इस topic के सम्बन्ध में कोई प्रश्न हो, तो आप हमसे comment box में पूछ सकते हैं. हम आपके प्रश्नों का उत्तर देने की कोशिश करेंगे।
