बरनौली प्रमेय (Bernoulli’s Theorem in Hindi) 1738 में डेनियल बरनौली ने दी थी. यह theorem ऊर्जा के संरक्षण (Conservation of Energy) के नियम पर आधारित है. इस theorem के अनुसार, “किसी बहने वाले द्रव्य की कुल यांत्रिक ऊर्जा यानी Mechanical Energy (दाब ऊर्जा (Pressure Energy), स्थितिज़ ऊर्जा (Potential Energy) और गतिज ऊर्जा (Kinetic Energy)) नियत (constant) रहती है.”
बरनौली प्रमेय का सिद्धांत (Principle of Bernoulli Theorem) आदर्श द्रव्य (Ideal Fluids) का प्रयोग करता है.
बरनौली समीकरण क्या है? | What is Bernoulli’s Theorem Equation in Hindi?
जैसा की ऊपर लिखी गयी definition में बताया गया है की दाब ऊर्जा, स्थितिज ऊर्जा और गतिज ऊर्जा का योग नियत यानी constant होता है. यह तीनों ऊर्जायें मिलकर यांत्रिक ऊर्जा बनाती हैं.
- आर्कमिडीज का सिद्धांत क्या है और यह कैसे काम करता है?
- किरचॉफ का नियम क्या है? | What is Kirchhoff’s Law in Hindi?
- ओम के नियम का सत्यापन करें।
दाब ऊर्जा (Pressure Energy) + गतिज ऊर्जा (Kinetic Energy) + स्थितिज ऊर्जा (Potential Energy) = नियत (Constant)
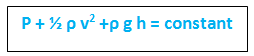
जहाँ, P = द्रव्य द्वारा बनाया जाने वाला दाब (Pressure Created by Fluid), v = द्रव्य का वेग (Velocity of fluid), ρ = द्रव्य का घनत्व (Fluid Density), h = द्रव्य सतह से ऊंचाई (height of the fluid from the ground), नीचे दिये गये चित्र को देखें।
बरनौली के प्रमेय को सिद्ध कीजिये। | Bernoulli’s Theorem Derivation in Hindi
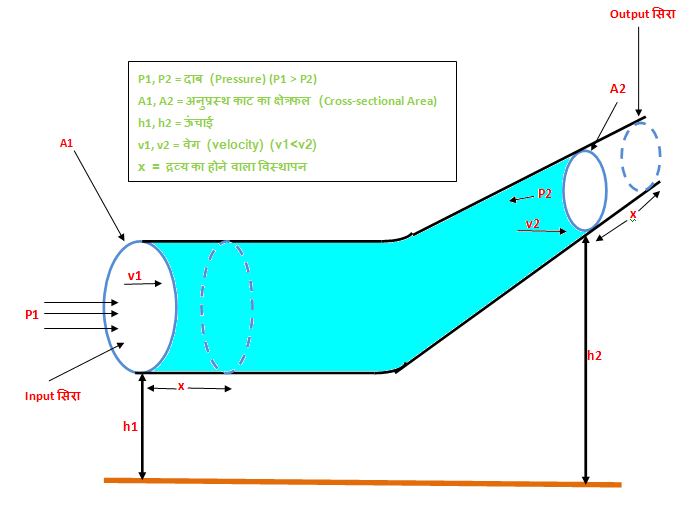
माना किसी पाइप के दो सिरे हैं, एक input सिरा, जिसका अनुप्रस्थ काट का क्षेत्रफल (cross-sectional area) A1 है, दूसरा output सिरा, जिसका अनुप्रस्थ काट का क्षेत्रफल (cross-sectional area) A2 है. Input सिरे पर दिया जाने वाला दाब (pressure) P1 और output सिरे पर प्राप्त होने वाला दाब (pressure) P2 है. Input सिरे के द्रव्य (Fluid) का वेग (velocity) v1 और output सिरे पर द्रव्य (fluid) का वेग (velocity) v2 है. पाइप से बहने वाले द्रव्य में तीन प्रकार की ऊर्जा है, दाब ऊर्जा (Pressure Energy), स्थितिज ऊर्जा (Potential Energy) और गतिज ऊर्जा (Kinetic Energy).

हम जानते हैं की, द्रव्य में PE (दाब ऊर्जा) = P × V
दाब ऊर्जा प्रति एकांक आयतन में = PE/ V ——————————————(1)
समीकरण (1) में PE का मान रखने पर,
दाब ऊर्जा प्रति एकांक आयतन = P × V/ V
दाब ऊर्जा प्रति एकांक आयतन = P ——————————————— (A)
दाब ऊर्जा प्रति एकांक द्रव्यमान में = PE/m
PE का मान रखने पर = P × V/ m
घनत्व के सूत्र के अनुसार, ρ = m/V, जहाँ, m = द्रव्यमान (mass) और V = आयतन (Volume)
दाब ऊर्जा (PE) प्रति एकांक द्रव्यमान में = P/ρ ————————————- (B)
हम पढ़ चुकें हैं, गतिज ऊर्जा (Kinetic Energy) (KE) = ½ m v2
गतिज ऊर्जा प्रति एकांक आयतन = KE/V
KE = ½ m v2 का मान ऊपर दी गई समीकरण में रखने पर,
गतिज ऊर्जा प्रति एकांक आयतन = ½ m v2/V
घनत्व के सूत्र से , ρ = m/V
गतिज ऊर्जा प्रति एकांक आयतन = 1/2 ρ v2 —————————————– (C)
गतिज ऊर्जा प्रति एकांक द्रव्यमान = गतिज ऊर्जा/m
गतिज ऊर्जा प्रति एकांक द्रव्यमान = ½ m v2 /m
गतिज ऊर्जा प्रति एकांक द्रव्यमान = ½ v2 ————————————— (D)
स्थितिज़ ऊर्जा (Potential Energy) = mgh
स्थितिज़ ऊर्जा प्रति एकांक आयतन = mgh/ V
स्थितिज़ ऊर्जा प्रति एकांक आयतन = ρ g h, ———————————- (E) चूँकि, घनत्व (ρ) = m/V
स्थितिज़ ऊर्जा प्रति एकांक द्रव्यमान = m g h/m
स्थितिज़ ऊर्जा प्रति एकांक द्रव्यमान = g h ————————————– (F)
ऊर्जा के सरंक्षण के नियम के अनुसार,
Input सिरे पर कुल ऊर्जा = Output सिरे पर कुल ऊर्जा
दाब ऊर्जा (Pressure Energy) = स्थितिज़ ऊर्जा (Potential Energy) + गतिज ऊर्जा (Kinetic Energy)
समीकरण (A), (E) और (C) से,
निकाय (system) में प्राप्त कुल दाब ऊर्जा (Total Pressure Energy) = P1-P2, क्योंकि, P1>P2
स्थितिज़ ऊर्जा में परिवर्तन = h2 ρ g – h1 ρ g
गतिज ऊर्जा में परिवर्तन = ½ ρ v22 – ½ ρ v12
P1-P2 = (h2 ρ g – h1 ρ g) + ½ ρ v22 – ½ ρ v12
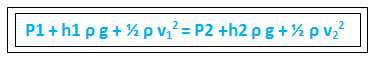
इस समीकरण से स्पष्ट है की बहते हुए द्रव्य में, किसी भी बिंदु पर ऊर्जा नियत होती है.
यदि h1=h2,
P1 + h ρ g + ½ ρ v12 = P2 +h ρ g + ½ ρ v22
P1 + ½ ρ v12 = P2 + ½ ρ v22 (G)
ऊपर समीकरण से यह स्पष्ट है है की यदि दाब (pressure) बढ़ेगा तो वेग (velocity) कम हो जायेगा।
बरनौली प्रमेय के क्याअनुप्रयोग हैं? | Application of Bernoulli’s Theorem in Hindi
वैसे तो barnauli ki pramey के कई अनुप्रयोग हैं, जिनमे से कुछ हम यहाँ discuss करेंगे,
Atomizer/Sprayer
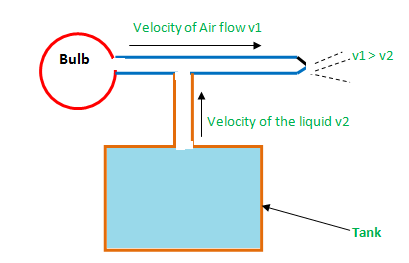
जब हम bulb को दबाते हैं तो एक हवा बहती है। उस हवा का वेग (velocity) v1, tank में भरे द्रव्य के वेग (velocity) v2 से ज्यादा होता है,तो pressure कम होगा। जिसके कारण Tank में भरा द्रव्य ऊपर की तरफ move करेगा। द्रव्य हवा के साथ mix हो जायेगा और spray से बाहर आ जायेगा।
Lifting of an Air Plane
हवाई जहाज के पंख हवा में ऊँचे उठते हैं, यह बरनौली प्रमेय पर आधारित है. नीचे दिए गए चित्र को देखें, हवा का कण (Air Particle) C, air particle A की तुलना में लम्बी दूरी तय करता है जबकि दोनों particles के द्वारा लगने वाला समय t है. ऐसा इसीलिए होता है क्योंकि ऊपर से पंख मुड़े हुए होतें हैं और निचे से सीधे होते है.
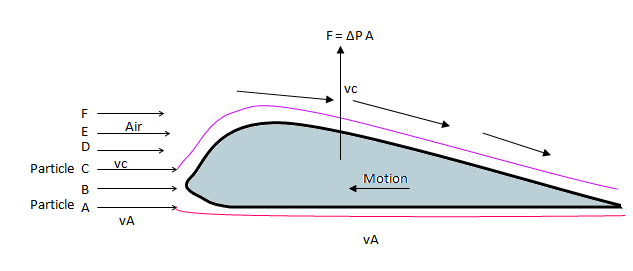
इसका मतलब यह है की particle A की velocity Particle C की velocity से कम है. (vc > vA). तभी दोनों ने एक ही समय t पर अलग अलग दूरी तय की है.
हवाई जहाज के पंख की shape एक velocity difference पैदा करती है.
Bernoulli Theorem के अनुसार (derivation में लिखे, समीकरण G से यह स्पष्ट होता है), यदि velocity बढ़ेगी तो pressure कम generate होगा। चित्र में देखें ऊपर की तरफ लगने वाला pressure (Phigher), नीचे की तरफ लगने वाले pressure (Plower) से कम है. (Plower > Phigher)
पंखों के लिफ्टिंग में लगने वाला Force = (Plower – Phigher) A
समीकरण G से,
Plower + ½ ρ v12 = Phigher + ½ ρ v22
Plower – Phigher = ½ ρ ( v22 – v12 )
ΔP . A = ½ ρ ( v22 – v12 )
F= ½ ρ ( v22 – v12 )
बरनौली प्रमेय के आधार पर मैगनस प्रभाव की व्याख्या कीजिये।
कभी आपने Cricket की Leather बॉल देखी है, उसमे टाँकें लगे होते हैं. कभी सोचा है ऐसा क्यों होता है? बॉल को curve देने के लिए. क्योंकि जब आप बॉल फेंकते हैं तो बॉल का curve वाला भाग हवा में तेजी से गति करता है और बॉल का दूसरा भाग हवा में धीमे गति करता है.

Curve वाले भाग पर पैदा होने वाला pressure कम होता है और दुसरे भाग पर pressure अधिक पैदा होता है. जिसके कारण यह सीधी गति नहीं करती। यह जमीनी सतह से टकराकर अपनी दिशा बदलता है.
Venturimeter और Pitot Tube भी बरनौली प्रमेय की दो application है. इनके बारे में अगले आर्टिकल में पढ़ेंगे।
